SPSS ile Ki-Kare Analizi

 

Merhabalar,

bu yazıda χ² istatistiğinden söz ediyorum. Araştırmalarımızda kategorik veriler arasındaki ilişkileri merak ettiğimiz zamanlar olmuştur. Örneğin öğretmenlerin cinsiyeti ile sınıfta kullandıkları öğretim yöntemleri arasında bir ilişki var mı diye sorabiliriz. Bu durumda cinsiyet ve sınıfta kullanılan öğretim yöntemi kategorik değişkenlerdir ve parametrik testler kullanarak bu ilişkileri göremeyiz. Bu tür kategorik veriler arasındaki ilişkileri belirlemede χ² (Chi-Square yani Ki-kare) istatistiğinden yararlanırız. Bu yazımınızın ve yukarıdaki videonun konusu χ² istatistiği. Aşağıdaki görselde χ² istatistiğinin zaman içinde nasıl geliştirildiğini ve Tek Değişkenli χ² istatistiği ile iki  değişken arasındaki ilişkileri incelediğimiz χ² istatistiği arasındaki farkı göstermek istedim.

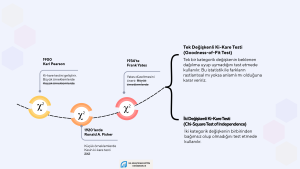
Karl Pearson, 1900’de ki-kare testini geliştirir. Temel amacı, gözlenen frekanslar ile beklenen frekanslar arasındaki farkın rastlantısal mı yoksa anlamlı mı olduğunu görmektir. Pearson’ın test istatistiği (χ²), aslında normal dağılımın bir türevidir. Bu nedenle Pearson’ın χ² testi örneklemin büyük olduğu ve beklenen frekansların yüksek olduğu durumlarda doğru sonuç verir. Ancak örneklemler ya da hücrelerdeki frekanslar küçükse doğru sonuç veremez. 1920’lerde Ronald A. Fisher küçük örneklemlerde kullanılabilecek, tam olasılıklı bir yöntem geliştirir. Fisher’ın Kesin Ki-Kare Testi olarak adlandırdığımız bu yöntem özellikle 2×2 tablolarında gözlenen frekansların 5’ten küçük olduğu durumlarda tercih edilir. 1934’te ise Frank Yates 2×2 tablolar için ki-kare testinin hatalı sonuç verdiğini fark eder ve Yates düzeltmesini önerir. Alan yazınında, Yates düzeltmesinin Tip II hata olasılığını artırabildiğine ilişkin bilgiler vardır. Bu nedenle geniş örneklemlerde Yates düzeltmesi gerekmeyebilir.

Bu yazıda iki tür χ² istatistiğinden söz edeceğim. Biri tek örneklem χ²  istatistiği, tek bir kategorik değişkenin beklenen dağılıma uyup uymadığını test etmede kullanılır. Bu istatistik ile farkların rastlantısal mı yoksa anlamlı mı olduğuna karar veririz. Diğeri, birden fazla kategorik değişken arasındaki ilişkileri incelediğimiz χ² testi (test of independence). Bu ise iki kategorik değişkenin birbirinden bağımsız olup olmadığını test etmede kullanılır.

Ki-Kare İstatistiğinde Kategori Sayısı

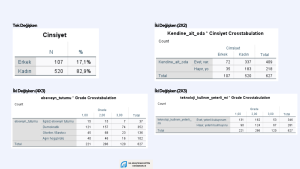
χ² testini yapmadan önce değişkenlerimizdeki kategori sayısını belirlemekte fayda var. Eğer tek değişkenle çalışıyorsak Tek Örneklem χ² testini kullanırız. Birden fazla değişken arasında ilişki olup olmadığını inceliyorsak, iki değişkenli χ² testini kullanırız. Aşağıda SPSS’te ürettiğim farklı değişkenlere ait tabloları görmektesiniz. İlk örnekte yalnızca cinsiyete ait frekansları görüyorsunuz.  Kadın ve erkek katılımcıların sayı bakımından, birbirinden önemli ölçüde farklı olup olmadığını kontrol edecek olduğumu varsayalım. Bu durumda bu tabloyu kullanarak tek örneklem χ² testi kullanabilirim. Sağlık alanında çoğu çalışmada örneklem özelliklerinin denkliğini sağlama konusunda kanıt ararken bu analizin sıklıkla kullanıldığını görebilirsiniz.

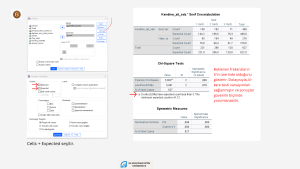
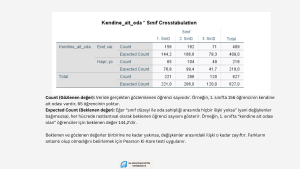
Diğer örneklerde ise birden fazla değişkene ait frekansları gösteren çapraz tablolar verdim. Mesela öğrencilerin kendilerine ait odalarının olması durumu ile cinsiyetleri arasında bir ilişki olup olmadığını incelediğimizi varsayalım. Bu durumda katılımcılara kendilerine ait odaları olup olmadığını evet-hayır yanıtı ile bildirmelerini istemişsek, bu değişkene ait iki kategorimiz vardır. Cinsiyet değişkenini de iki kategorili olarak elde ettiysek, bu değişkene ait yine iki kategorimiz vardır. Bu durumda 2X2’lik bir tablo oluşturduk. Bir diğer örneği incelediğimizde ise katılımcılara algıladıkları ebeveyn tutumlarını sorduğumuz ve dört kategoride farklı yanıtlar elde ettiğimizi varsayalım. Sınıf düzeyinin ise üç kategorisi varsa, bu durumda 4×3’lük bir çapraz tablo oluşturmuş oluruz. χ² testi hesaplanırken gözenek sayıları önemlidir. Test sonuçlarının gözenek sayıları ve örneklem büyüklüğüyle ilişkili olabileceğini bilmekte fayda var.

 

Tek Örneklem (Tek Yönlü) Ki-Kare Testi (Goodness-of-Fit Test)

Tek Yönlü Ki-Kare Testi, bir değişkenin belirli kategorilere nasıl dağıldığını anlamamıza yardımcı olan önemli bir istatistiksel testtir. Özellikle belirli bir kategorik değişkenin gözlenen frekanslarının beklenen dağılımla ne kadar uyumlu olduğunu test etmek için kullanılır. Aşağıdaki görselde, SPSS kullanarak Tek Örneklem Ki-Kare Testinin nasıl yapılacağı göstermek istedim. Testin temel amacını, ne zaman kullanılması gerektiğini, varsayımlarını ve SPSS üzerinden nasıl uygulanacağını görsellerle desteklemenin yararlı olacağını düşündüm. Ayrıca sayfanın altında yeni oluşturduğum başka görsellerle de aynı konuyu açıkladım. Onları da incelemeniz yararlı olabilir.

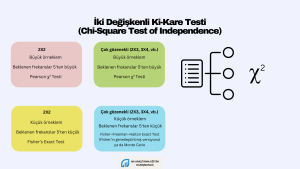
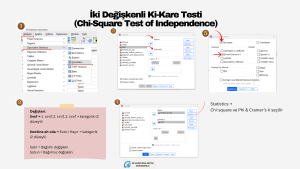
İki Değişkenli Ki-Kare Testi (Chi-Square Test of Independence)

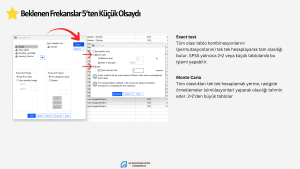
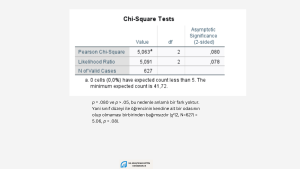
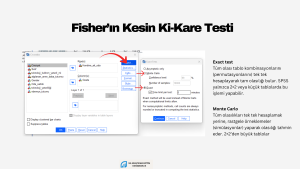
Birden fazla kategorik değişken arasında ilişki olup olmadığını incelemek istiyorsak, χ² testi kullanabiliriz. Örneklem büyüklüğünün ve değişkenlere ait kategori sayılarının sonuçları etkileyebileceğini bilmekte yarar var. Örneğin büyük bir örneklemimiz varsa, 2X2’lik ya da daha fazla gözenekli bir tablo oluşturmuşsak ve gözeneklerdeki beklenen frekanslar 5’ten daha küçük değilse ya da bunların oranı %20’den azsa, Pearson χ² testini kullanabiliriz. Küçük bir örneklemden veri toplamışsak, 2X2’lik ya da daha çok gözenekli bir tablomuz varsa Fisher’ın Exact testini kullanırız. SPSS çok gözenekli, küçük örneklemli analizler için Fisher’ın Exact testi yerine Fisher’ın genelleştirilmiş versiyonu olan Fisher–Freeman–Halton Exact Testini hesaplar. Ayrıca bu tür durumlarda Monte Carlo’yu da kullanabilirsiniz. Hangi istatistiği kullandığınızı raporlamanızı öneririm.

χ² İstatistiğinin Kullanımında Olası Hatalar

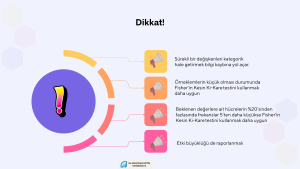
• Elimizde sürekli bir değişken varsa (örneğin öğrencilerin test puanları gibi) bunları kategorize etmek önemli bilgi kayıplarına neden olur ve ayrıca yapay bir anlamlılık ortaya çıkabilir. Sürekli değişkenler için, araştırmanın amacına bağlı olarak t-Testi, ANOVA, regresyon gibi analizler daha uygun olabilir.
• Örneklemlerin küçük olması durumunda Pearson χ² istatistiği hatalı sonuçlar verebilir. Bunun yerine Fisher’in Kesin χ² testini kullanmak daha uygun bir yoldur.
• Hücrelerin %20’sinden fazlasında frekanslar 5’ten daha küçükse Pearson χ² istatistiği hatalı sonuçlar verebilir. Bu durumda Fisher’in Kesin χ² testini ya da Monte Carlo kullanmak daha uygun olabilir.
• Sadece anlamlılık düzeyine dayalı yorum yapmak eksik bir yaklaşım olarak değerlendirilmelidir. Etki büyüklüğü de raporlanmalıdır.

Etki Büyüklüğünü Nasıl Yorumlayalım?

Tek Örneklem χ² istatistiği için SPSS etki büyüklüğünü hesaplamıyor. Son versiyonunda bu özellik geldi mi bilmiyorum tabi. Kontrol etmekte fayda var. Ben 27 sürümü kullanıyorum ve bu versiyonda tek örneklem Ki-kare için etki büyüklüğü seçeneği yok. Bu durumda elde hesaplama yapabilirsiniz. Aşağıdaki görselde formülünü de verdim. İki  değişken arasındaki ilişkileri araştırdığımız durumlar için SPSS etki büyüklüğünü hesaplayabiliyor.

Tek Örneklem Ki-Kare Testinde Etki Büyüklüğü

Tek örneklem χ² istatistiğine dayalı olarak gözlenen dağılım ile beklenen dağılım arasında fark varsa, bu farkın, hangi önem düzeyinde olduğunu belirlemek yani etki büyüklüğünü hesaplamak için Cohen’in w katsayısını kullanabilirsiniz. Bu katsayı hesaplanırken elde ettiğiniz χ² değerini örneklem büyüklüğüne böler ve karekökünü alırız. Oldukça basit bir yolla hesaplamamız mümkün olduğundan, SPSS’in bu katsayıyı hesaplamamasını dert etmeye gerek olmadığını düşünüyorum 🙂

İki Değişkenli Ki-Kare Testinde Etki Büyüklüğü

Cramer’in V katsayısını ya da Phi (φ) katsayısını raporlayarak etki büyüklüğü hakkında okuyuculara bilgi verebilirsiniz. Phi (φ) katsayısı yalnızca 2×2 tablolar için uygundur. Cramer’in V katsayısı ise daha büyük tablolarda kullanılır. 2×2 tablolarda etki büyüklüğünü yorumlamada Cohen’in (1988) belirttiği ölçütlere dayanarak  .10 küçük etki büyüklüğü, .30 orta etki büyüklüğü ve .50 büyük etki büyüklüğü olarak yorumlanabilir. Cramer’in V katsayısını yorumlarken Cohen’in ölçütleri uygun olmayabilir. Çünkü 5×4’lük bir tabloda .28 orta etki büyüklüğü anlamına gelebilir. Bu nedenle bu ölçütleri katı bir eşik değeri olarak yorumlamak yerine referans aralığı olarak vererek, tartışmak uygun bir yol olabilir.

SPSS ile χ² Hesaplayalım

İlk olarak bir örnek veri seti vererek başlamak istiyorum. Böylece sizler de yazının üstüne eklediğim videoyu izleyerek ya da aşağıda eklediğim görselleri inceleyerek analizleri yapabilirsiniz. Ayrıca sonuçları nasıl yorumlayacağınıza ilişkin küçük ipuçları içeren görselleri de eklemeyi unutmadım.

Örnek veri seti için tıklayın.→Ki_Kare_Örnek_Veri_Seti

 

 

Kılavuz sayfaya dönmek için buraya tıklayın.

Sevgiler

Doç. Dr. Fatma Betül KURNAZ

Okuma Önerileri ve Kaynaklar

Berkson, J. (1938). Some difficulties of interpretation encountered in the application of the chi-square test. Journal of the American Statistical Association, 33(203), 526–536.

Bolboacă, S. D., Jäntschi, L., Sestraş, A. F., Sestraş, R. E., & Pamfil, D. C. (2011). Pearson–Fisher chi-square statistic revisited. Information, 2(3), 528–545.

Camilli, G., & Hopkins, K. D. (1978). Applicability of chi-square to 2 × 2 contingency tables with small expected cell frequencies. Psychological Bulletin, 85(1), 163–167.

Corder, G. W., & Foreman, D. I. (2009). Nonparametric statistics for non-statisticians: A step-by-step approach. Hoboken, NJ: Wiley.

Delucchi, K. L. (1983). The use and misuse of chi-square in social science research. Social Science Research, 12(1), 61–75.

Lewis, D., & Burke, C. J. (1949). The use and misuse of the chi-square test. Psychological Bulletin, 46(6), 433–459.

McHugh, M. L. (2013). The chi-square test of independence. Biochemia Medica, 23(2), 143–149.